Two. The number of things that broke in my apartment yesterday.
Actually. Three. If you count my heart.
Negative sixty-seven. How functional my oven is right now on a scale of 1 to10.
Negative sixty-seven. How functional my hypothalamus is right now on a scale of 1 to 10.
Twenty-four. The number of coverslips of cells I had to electroporate yesterday. Even in the wake of my broken oven and the fever, aches, pains, and chills that ensued from the discovery of my broken oven.
Two. The number of Advils I took to deal with the fever, aches, pains, and chills that ensued immediately after the discovery my broken oven. Oh hypothalamus. Why do you hate me so?
Thirty-eight. The number maintenance requests that I have submitted so far. At least one for every hour of the day that I’ve had to live without an oven. Sometimes more. Depending on whether my fever was high enough that I forgot I had already submitted a maintenance request that hour.
Five. The number of times I tried to convince my parents that, no. My fever was not due to “bad air”. But to a psychological and emotional connection I had with my oven. Such that when it broke. My hypothalamus thought, Hey! Wait for me! I want to go straight to hell too!
Ten. The number of dreams I had last night that revolved around this white chocolate raspberry truffle cheesecake. That I baked last month for Adam’s birthday.
Those were the days.
One. The number of ice cream makers that I put in my freezer. Because the only way I know how to deal with stress like this is to bake. And those who can’t bake. Make ice cream. Stay tuned.
When I tell you that this is the best cheesecake I’ve ever made. That when I say I’m upset about my oven for a variety of different reasons, what I really mean is that I’m upset really and truly because it means that I can’t bake this cheesecake again in the near future. You are going to have to trust that I’m not just hyperbolizing. Or exaggerating the past. And then you are going to have to get in the kitchen. Turn on your oven (oh how I envy you!). And start baking.
You can do that for a poor, hypothalamus- and heart-broken girl living on the upper east side without a working oven. Can’t you?
White Chocolate Raspberry Truffle Cheesecake
Serves 16, adapted from Dinner and Dessert
Crust
1 1/2 cups chocolate graham cracker crumbs (I used these adorable graham cracker cookies from Whole Foods. They were shaped like rabbits.)
1/3 cup butter, melted
Filling
1/2 cup raspberry preserves
1/4 cup water
32 oz 1/3 Less Fat Philadelphia cream cheese, softened
1 1/4 cups sugar
1/2 cup sour cream
2 tsp vanilla extract
5 eggs
4 oz white chocolate chunks
1. Preheat oven to 475. Create a water bath by placing a large pan filled with about a half a cup of water into the oven while it preheats. Before you do this, though, make sure your springform pan fits into the water bath pan. Otherwise you’ll be in for a fun surprise in a few steps.
2. Combine the raspberry preserves with a 1/4 cup water in a microwave safe bowl and microwave for 1 1/2 minutes. Stir until smooth. Strain to remove the raspberry seeds, then let cool.
3. Measure 1 1/2 cups of chocolate cookie crumbs into a bowl. Pour the melted butter into this bowl and mix. Press the crumbs into a 10-inch springform pan. Wrap a large piece of foil around the bottom of the pan. Put the crust in your freezer until the filling is done.
4. Use an electric mixer to combine the sugar with the cream cheese, sour cream, and vanilla. Mix until smooth and creamy. Scrape down the sides of the bowl. In a separate bowl, whisk together the eggs and then add them to the cream cheese mixture. Blend until just incorporated.
5. Remove the crust from the freezer and sprinkle the white chocolate chunks on top of it. Pour the cream cheese filling into the crust. Pour dollops of the raspberry preserves around the crust in a circle. Drag a toothpick through them in order to get the swirl shown above.
6. Carefully place the cheesecake into the water bath. Bake for 12 minutes. Then, lower the oven to 350 and bake for 60-90 minutes or until the top of the cheesecake turns a light brown or tan color.
7. Remove from the oven to cool. When cool, put in the refrigerator for at least four hours or overnight.
Be sure to send me your entries to Regional Recipes: Ethiopia by July 31st!













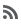


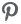







Oh wow…I hope your heart is broken over your oven and not any other reasons…actually I don’t HOPE your heart is broken, but you know what I mean. Ok- that sounded dumb.
Anyway…cheesecake looks amazing and hot ovens in summer are overrated…your oven knew it and went on strike 😉
Oh no…that totally sucks!! Sending healing thoughts your way…and your oven’s way…and dreaming of one slice of your mouthwatering cheesecake in the meantime. I’m pretty sure the ice cream will make you feel better…if only for a fleeting moment 😉
wow, that looks amazing! Gosh, I don’t know what I would do if the oven broke! ah! I hope it gets fixed soon!!!
There there, Joanne’s hypothalamus … everything will be just fine. Poor thing.
And poor Joanne! Being without an oven, for even a moment … how will you create?? I guess this could be a good thing, since it’s so hot around here, ice cream is definitely preferable to oven -baked goods…? Ok, never mind, I take it back! You NEED an oven! Crossing my fingers that it’s back in your life SOON!
This looks soo very scrumptious Joanne.
Oh, that stinks! Isn’t funny how when things like that break you all of a sudden want to bake the crap out of everything and it just makes you angrier! I hope it gets fixed soon! This looks beautiful BTW! Cheesecake is one of my favorites!
Oh Good Golly that looks good (just read Dave’s blog, loved his words) Joanne that cheesecake looks amazing. As always, great photos. And that just sucks about your oven.
Cheesecake mmm, my husband would love a piece of it. He is great fan. It looks gorgeous. Sorry about your oven, but hey life is too short to be emotionaly stressed for such things. Cheer up!
amazing cheesecake and u always make me smile hope oven gets fixed ASAP
OMG, that cheesecake looks good! I would totally eat a piece for breakfast. Oh, and I’m sending prayers for your oven’s speedy recovery 🙂
Ok, I’m laughing AND crying! I feel your pain, truly I do. I foodie being without an oven? Unheard of!
Would it help if I told you that the first four onths we lived in our house, all I had was a microwave, a crock pot and an electric skillet?
FOUR. MONTHS.
AWWWW, all those numbers, you deserve some 69..
ABSOLUTELY LOVE THE CHEESECAKE!!
cheese cake looks so lovely
Hey, Chin up! Someone will come over to fix that oven. Lovely cheesecake and it does look fabulous. I will take your word that this in fact is the best cheesecake you baked.
Oh darling, your heart is broken, your oven is broken, this hopefully will be over soon.
p.s
your cheesecake look so good. Raspberry and chocolate are meant to make you happy, even if your heart broken (at least a little)
fever and a broken oven 🙁
thats terrible news!! im praying to the oven gods to fix it ASAP!! <3
a truffle cheesecake.. wow! ur creative mind keeps getting more incredible!
xo
Your cheesecake looks and sounds luscious, Joanne. Hope that oven is soon repaired and the fever goes away. It’s no fun to be sick at this time of year. Take care…Mary
Oh dear! How utterly annoying. You must be cheweing nails along with your chills and fever.
Too bad you couldn’t be eating this divine cheesecake, Joanne. Wow. Raspberries and chocolate are just meant to be together. Always have thought so. And how cute are those bunny grahams at Whole Foods??
Send you a big “HUG” and hope you are better now. Love the design you created with the raspberry preserves. Did you notice that the centre looks like a cute little girl’s face? Hehehe! 😉
I lasted about one week total when my oven died. And after asking my husband repeatedly to get me another one and him not responding, I decided to buy one on line and have it delivered to my house. I had the man put the huge double oven box right in the walkway to the kitchen. (The only way to get a man to do what you want sometimes is to inconvenience him.) It was up and in my wall within 2 hours of him getting home that day! I rewarded him with baked goods from the gods : )
Your cheesecake looks heavenly. I love white chocolate with raspberries : )
I know how that feels….even when everything just seems so bad, know that eventually things will work out…even with your patients and electroporation experiments….
that looks amazing, and i hope your oven gets fixed soon!!! i might have to request this as my bday cake… 😉
Actually, baking in 90 degree heat isn’t that much fun anyway. Just keep telling yourself that until it’s fixed! At least you have wonderful cheesecake memories – and delicous ones, I might add.
There is some nasty bug rooming about these days – I had it Friday-Sunday but I’m feeling better today. I hope you are feeling better soon too!
I hope this comment doesn’t come through twice…anyway, my suggestion is a bit shady, but you can go purchase a toaster oven (which I use all the time to make cakes and cookies) until your oven is fixed, and then you can return it. I know how terrible that is, and I’ve never done this (I swear) but Ali has been known to purchase a router/dsl box in a pinch and then return it.
I hope you feel better soon!
Hey Joanne, your’e so funny, and your cake looks awesome despite your oven problems. Sorry about that, by the way. Oven issues are common, so don’t let it get you down. Mine sucks too!
Hope you feel better. Stella
SO sorry about your oven! That is a bummer. I hope the ice cream cheered you up at least a little bit.
This cheesecake looks so delicious. I rarely crave cheesecake but after looking at these luscious photos I am totally considering making one now.
At least the oven went out during the summer when we eat more salads. I would DIE if it went out in the winter… not being able to roast things would kill me. The cheescake looks heavenly!!!
Joanne,
Three. The number of reasons why this cake is marvelous. Great recipe, cooked to perfection, beautifully shot.
Feel better
Hey Joanne ! How you doin’ ? Missed a lot of yummies from your site..Just gopt back after my vacation…
This looks like a piece of heaven on plate…too good..
So impressive that you can make so few ingredients look so so sooooo fabulous!
Donna
I am really not a cheesecake girl, so I’ll have to trust you on this one. I’ll take your ice cream though! Sorry about the oven and hope broken things are soon fixed.
Oh you poor thing!! Though I am looking forward to some ice cream!
Joanne, sorry to hear about your oven 🙁
But the cheesecake with white chocolate and raspberry looks fabulous 🙂
ice cream cures all. broken hearts, broken stoves, broken bodies, i’ve even heard it cures broken toes which you should probably look into being you’re going to be a doctor and all..
You poor thing, I hope everything improves, asap! At least you have this incredible cheesecake for comfort… It looks like it could be the most potent pain killer of all. 🙂
What a stunning cheesecake! I’m in love with the swirl and how it looks like there are little hearts. And I love that there’s white chocolate in the cheesecake too. I might just have to make this soon! It’s been too long since I’ve made cheesecake.
SO sorry about your broken oven, Joanne! Grrr, that would be SO frustrating! I’m happy you have ice cream to drown your sorrows, and hope for a fully-functioning baking mecca for you soon. 🙂
I can’t get over how gorgeous this cheesecake looks. I can only imagine how good it tastes. Bravo my friend.
UM, HELLO. LOVER. Get a load of that cheesecake. Damn me for not living next door to you. But my oven is still operational…
Now, why the broken heart? DISLIKE. Do I need to beat someone up?
sorry about the oven, dear. this recipe is two steps away from being porn. seriously. YES PLEASE!
xo Alison
Nothing soothes the soul better than cheesecake, and your pics are outta sight. I’m printing this one and it’s going into the cue for those occasional “Gary needs to be made whole again” days
looks divine..feel like grabbing that slice from the screen and indulge myself..yumm…
Um, I think I just drooled at my computer. Yeah, whoops.
Perhaps you can get an entire oven upgrade, instead of just a repair? Upgrades are good, right?
You know what I’m thinking? I’m thinking you need a toaster oven (if you have room). I don’t know if it’s a possibility for you, but a lot of people really like them. In the summertime my friend uses her toaster oven instead of turning on her oven. She’s convinced it puts off less heat.
On another note, this cheesecake is making me DROOL! I love the white chocolate and raspberry combo, especially with the chocolate crust. I think this dessert covers all my favorites:)
okay, all my favorites….except peanut butter- LOL! Hmmm…peanut butter cheesecake.
I’m so sorry about your broken oven, and heart. Thank goodness for sweet memories 🙂
Cheesecake is one of my all-time fav’s! Yours looks incredible. I have to try this one. I am posting a cheesecake next; we are on the same wave length:)
I feel for you that your oven is broken; that is bad news for us bloggers. I know you will come up with some amazing, no-oven ideas. Looking forward to the ice cream. My camera is broken and I have been using my daughters; another blogger nightmare.
sigh~ it is frustrating when things aren’t working…but this cheesecake! whew! i am sure it can heal any broken heart in no time!
This comment has been removed by the author.
Gah, this looks gorgeous! I can’t wait to have an occasion to serve this beast! 🙂
woo hoo, what a luscious looking cheesecake.. I am loving the gorgeous flavors of white chocolate and raspberry… Yumm…
Your oven will get fixed in no time… Enjoy the Summer. Have fun gal.
Not going to lie. When I first saw this post I was a little peeved I didn’t get invited to the cheesecake party especially since it looks and sounds sensational. But then I kept reading and realized this was before my time. Friendship intact. How’s your fever/chills/etc? And your oven, more importantly. How’s your OVEN?!
Being without an oven is the worst. It is right up there with being without a dryer after you washed your clothes. Weak! Your parents sound like mine with the ‘bad air’ or ‘wet hair’ causing all ailments. LOL. Your cheesecake would make anyone feel better. Mind sending me a slice…or 12?
I always hated having to come up with a good hypothalamus for a science project. What? not that?
Oh, yeah, geometry, I hated trying to figure out the hypothalamus of a triangle. Still no?
Well my oven works so bite me! 🙂 😉 :0
I think when your oven is working again you should make a few of these and freeze them…just in case! But really…that does suck. I feel your pain…My parents won’t let me so much as look at the oven. It’s off limits until it gets cooler…so it might as well be broken. I am in love with this cheesecake too! Totally delectable!
Wow this is incredible beautiful. I may need to make this version for my good friend. she love raspberry, white chocolate and cheesecake
When I got married and moved into my husbands fix it up home we had this old jen air (still gives me goosebumps”. The only way to change the temp was with a pair of pliers, god forbid recipes with varied temps, but them the nob broke off entirely and I was stuck with a 250 deg oven. Kitchen was the first room we remodeled.
Oh no! I feel your pain girl. I hope everything starts looking up soon! Your cheesecake has me drooling. You are in my thoughts.
Hang in there & get some rest! You will need the energy when that oven gets fixed and you are back to baking fabulous cheesecakes – that one is GORGEOUS! Feel better:)
What happens if the oven is working fine but I just don’t bake? Get the cheesecake from Joanne 🙂
white chocolate? truffle? WOW! Looks so good. My dad makes great cheesecake too but I have to ask you since you are an expert… is it gross to eat cheesecake at room temp? My dad loves it that way and I think that that’s possibly the grossest thing EVER! I never eat it til the next day. UGH!!
Oh lordie. Hope both your oven and body are better soon, Joanne! As for this wonder of a baked good, I can simply stare…and drool.
I used to work in property management. Shame on them for not fixing your poor oven yet! This is totally unacceptable. Don’t they know you have a blog to run?! So sorry you aren’t feeling well. Get well soon! This is a completely gorgeous cheesecake!
Hope you and your oven are feeling much better soon. 😉 The cheesecake looks amazing.
what a shame that so many negative things ended up being associated with this AMAZING cheesecake. it’s truly my ideal flavor combination, and the little surprise hearts in the swirls make it even more outstanding.
get well soon!
yummy cake looks great i love this post
http://smsjar.blogspot.com/
White chocolate and raspberry…what a combination! Absolutely gorgeous!
Talk about cheesecake!! This one looks divine!! So sorry about your broken oven 🙁 Electroporating cells all day definitely requires coming home to a working oven..lol. At least you have ICE CREAM, that makes everything mo’betta 🙂
that looks totally amazing, cheesecake is my fav!!! I am so sorry about your oven and you feeling sick, feel better!
How do you manage to write great posts with fever and broken heart & oven? I hope you are feeling better now.
The cheesecake looks amazing, raspberry-white chocolate is one of my favourite combination! Would love to try soon… but,first, there are some ethiopian dishes on my list 😉
zero: the number of problems you have now, because cheesecake – especially with white chocolate and raspberries – should fix them all!
Hope you are feeling better soon 🙂
Une pure gourmandise. J’adore.
Bonne semaine et à bientôt.
Everyone has to stop making cheesecake… I’m dying here. I would kill for a slice of this! Cheesecake is one of those things that I just can’t resist.
That first picture is stunning, Joanne. You did a fantastic job!
I am so sorry about the oven! But hey, look on the bright side: a broken oven can’t make your apartment even more hot and sticky than it already is! I love to bake but have had trouble doing so in this heat. It just gives you an excuse to eat lots of cold desserts, like ice cream, as you mentioned. And smoothies. You should consume many, many smoothies.
Love that you used the low fat cream cheese. Oven or not, this still looks like a success!
Thank goodness you have a secondary plan for making treats. I can’t wait to see the ice cream you must be churning out like crazy. Here’s hoping the maintenance man isn’t blocking your number and that you have a working oven soon.
Oh no, that sucks! Your cheesecake sounds absolutely amazing! with my fav white choc…yum
Did you try kicking the oven? Sometimes a good kick is just what it needs! Your cheesecake is to die for though! It really looks delicious! Hope you get rid of that fever soon!
hi Joanne
first I hope your heart is only broken because of the oven…..that cheesecake looks so very very good! the texture, colour are a wow! your images are fantastic…..I do hope you get your oven back soon…but in the mean time I’ll wait for your ice cream!
Dennis
White chocolate and raspberry and cheesecake. Yes, I’ll have that for dessert, please! Looks amazing. Good luck with your oven repair.
at least you got this beauty out and cooked before the oven broke!
Get thee a new oven, girl! This cheesecake looks to good to be a one-night stand. You need a life-long relationship with this beauty. 😉
noooo….not the oven!!! I feel for you. Been there…done that. There’s only so much you can do on a grill and / or microwave.
this cheesecake….holy moly!!!
I don’t think I’ve ever heard the word hyperbolizing before. Makes sense though. I’m just trying to get my mind of the most amazing cheesecake in the world!! Another blogger just asked what our favorite food was. CHEESECAKE! Yes, absolute favorite in the whole wide world. Not hyperbolizing in the least!
I had the oven break once and while I cried at first I think it just opened my foodie mind to other alternatives. But I do hope you get it fixed soon! and this cheesecake…oh my goodness it looks/sounds so good!!! great job!
I lived in an apartment where everything was broke every other day…When the oven broke I was upset…when the stairs to my bedroom collapsed with me on them…they let me out of the lease…It was not a cheap place either…I hope they get your oven fixed soon!
So sorry about your oven. I have an extra and wish I could send it your way. So glad it was working when you made this lovely cheesecake though. I haven’t had breakfast yet and it’s making me seriously hungry. I hope that the ice cream banishes your blues and makes everything better!
I hope you feel better, oh man I went two weeks without my oven and I almost died…i feel ya, loveing the cheescake..
sweetlife
I want I want I want. So sad about your oven =( Hot damn, you were lucky to get this amazing cake finished though!
This looks like a delicious cheese cake! Sorry about your broken oven, I hope it gets fixed soon.
Sounds like a rough one. I hope the cheesecake helped out. It looks wonderful!
Now that’s a gorgeous cheesecake! I hope both you and your oven are feeling better now 🙂
That’s one beautiful cheesecake. I was surprised it was made with raspberry preserves… makes it easy! Praying for you and your oven 🙂
I completely feel for you! That’s how I feel with no oven right now but someone is coming to fix it tomorrow! Not to rub it in or anything…but I will try and make this cheesecake to salve your wounded oven-less soul. This looks amazing. I can almost taste the smooth creamy velvety cream cheese…
Great job at the cheesecake.
oh my!
can i just say, what a great blog!!!
and now, the cheesecake! the cheesecake looks absolutelyyyyyyy amazing!!
Please! how can I just print the recipe????? I sooooo want to make that gorgeous cheesecake!
[…] Three years ago…White Chocolate Raspberry Truffle Cheesecake […]